- منو دسته بندی
- محصولات
- اطلاعیه
- توشه علمی
دانلود سوالات کنکورانیمیشن های آموزشیگروه های درسیالمپیاد - دفتر مشاوره
- سرگرمی
- با مهروماه
الف) ۱۰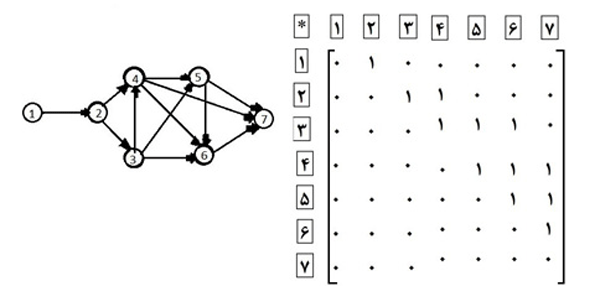 
چون مسیر ها در واقع از ۲ شروع می شود در کل ۱۱ مسیر داریم . قسمت ۱ به ۲ در همه مسیر ها مشترک است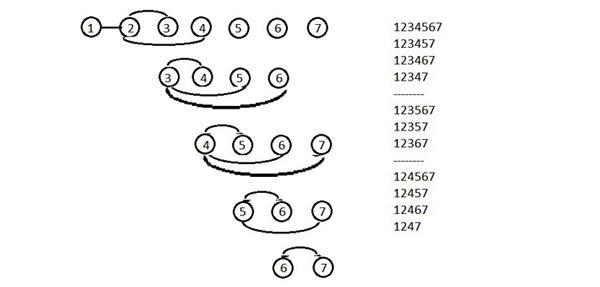
ارسال مطلب به ایمیل دوستاتون:
